Artículos | Formales | Matemáticas

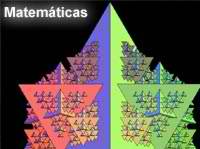
Casi tres décadas después de que el matemático Benoit Mandelbrot acuñara el término, todavía se desconoce mucho de su funcionamiento. Hace unos años, estaban de moda. Ahora parece que pasen de puntillas por los medios de comunicación.

"La investigación en fractales es un gran campo de las matemáticas conocido como sistemas dinámicos y la teoría del caos, por tanto, surge en cualquier ámbito de la ciencia, desde la biología a la química o la ingeniería. Se ha progresado en el conocimiento, pero dado que los fractales se encuentran en tantos campos, hay mucho que hacer", dice el matemático Robert Devaney, de la Universidad de Boston, que ha impartido una conferencia en Barcelona, invitado por la Obra Social La Caixa.

"En la mayoría de campos científicos, en la ingeniería, todo el mundo pensaba que todo debía ser previsible y que, por ejemplo, una reacción química no podía tener un comportamiento caótico", dice Devaney.

Uno de los ámbitos en los que se ha pensado aplicar la teoría de los fractales es la meteorología. ¿Por qué es tan complicado predecir el tiempo a medio plazo, a partir de tres a cinco días? "Es necesario entender cómo funciona cada molécula del aire, es imposible, y por tanto los científicos intentan realizar predicciones más simples, con fractales, que puedan ayudar a entender qué es lo que está pasando en una situación meteorológica". Reconoce Devaney que los investigadores aún trabajan en los fractales más simples, en los conjuntos de Mandelbrot, "que son muy bellos". "Pero si aún no los entendemos bien, ¿cómo podemos predecir el tiempo, que se mueve en variables infinitas? El camino es muy largo", añade.

El conjunto de Mandelbrot se basa en unas expresiones matemáticas simples (x2

+c) que producen hermosas y complicadas imágenes, cada una de ellas con significados matemáticos propios. El problema es que sólo es posible entender completamente esa ecuación si el límite del conjunto de Mandelbrot está localmente conectado, y hasta ahora nadie sabe si esto es cierto.

Los fractales pueden funcionar bien en biología, para analizar los tumores, dicen los expertos: "Si las células cancerosas son benignas, entonces el fractal es muy redondo; pero si el cáncer es maligno, si se extiende, el fractal será diferente. Y tenemos herramientas que miden cuál será la dimensión fractal del conjunto y determinan si el cáncer hace metástasis. Por tanto, los fractales son una herramienta matemática de la medicina", explica. Devaney participa en algunas reuniones mensuales que hacen en Boston un equipo de biomédicos, discuten sobre el caos y los fractales y cómo pueden incidir éstos en la medicina.

En España también hay varias iniciativas empresariales que utilizan los fractales en el desarrollo de productos: por ejemplo, una empresa nacida en la Universidad Politécnica de Cataluña ha creado unas antenas fractales capaces de enlazar señales de varias bandas de telecomunicaciones simultáneamente.

Publicado originalmente en El País (España)