Artículos | Espaciales | Astrof�sica

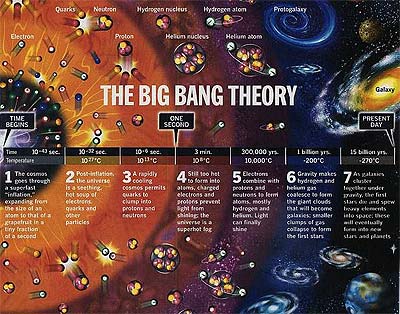
No hab�a planetas, estrellas ni galaxias; s�lo hab�a una mel� de part�culas elementales; �stas llenaban el Universo. Adem�s, todo el Universo era m�s peque�o que la punta de un alfiler y estaba incre�blemente caliente. De repente empez� a expandirse, y a medida que se extend�a a partir de este inicio extra�o e inesperado, evolucion� hasta el Universo que vemos hoy.

La ciencia moderna es incapaz de describir o explicar algo que sucedi� en los primeros 10-43 segundos despu�s del Big Bang. Este intervalo, 10-43 segundos, se conoce como el tiempo de Planck, con el nombre del cient�fico alem�n Max Karl Ernst Planck. �l fue el primero en introducir la idea de que la energ�a pod�a considerarse no como un flujo continuo, sino como paquetes, o "cuantos", cada uno de ellos con una energ�a espec�fica. La teor�a cu�ntica est� ahora en la base de gran parte de la f�sica moderna: trata del Universo en las escalas m�s peque�as y es ciertamente uno de los dos grandes logros de la ciencia te�rica del siglo XX. El otro es la teor�a de la relatividad general de Einstein, que trata de la f�sica de escalas muy grandes -escalas astron�micas, de hecho.

Pese a que, en sus propios dominios, ambas teor�as est�n extraordinariamente bien comprobadas por experimentos y observaciones, hay problemas importantes para reconciliar estas teor�as entre s�. En particular, ellas tratan el tiempo de maneras fundamentalmente diferentes. Las teor�as de Einstein tratan el tiempo como una coordenada; por lo tanto es continuo, y nos movemos suavemente de un instante al siguiente. En la teor�a cu�ntica, sin embargo, el tiempo de Planck representa un l�mite fundamental: la menor unidad de tiempo de la que se puede decir que tiene significado, y la menor unidad que podr�a medirse alguna vez, siquiera en teor�a. Incluso si construimos el reloj m�s preciso posible, lo ver�amos saltar bastante err�ticamente de un tiempo de Planck al siguiente.

Tratar de reconciliar estas dos visiones del tiempo en conflicto es uno de los mayores desaf�os de la f�sica del siglo XXI (recientemente intentado en la "teor�a de cuerdas" y su pariente la "teor�a de membranas"). Por ahora, en el Universo peque�o, caliente y denso que exist�a inmediatamente despu�s del Big Bang, la f�sica cu�ntica domina, y con ello empezamos nuestro estudio cient�fico del Universo 10-43 segundos despu�s del comienzo.

El Big Bang es una idea contraintuitiva. Nuestro sentido com�n parece mucho m�s inclinado a la idea de un Universo est�tico e infinito, y pese a todo hay buenas razones cient�ficas para creer en este suceso singular. Si aceptamos el Big Bang, es posible rastrear la secuencia completa de sucesos desde el primer tiempo de Planck hasta el presente, donde nos encontramos en lo que Carl Sagan describi� memorablemente como nuestro "punto azul p�lido".

El principio del tiempo

Por lo tanto, retrocedamos hasta el mismo inicio del Universo, inmediatamente despu�s del propio Big Bang. Es tentador imaginar que el Universo estalla de repente en un enorme oc�ano de espacio, pero esto es completamente err�neo. La verdadera imagen del Big Bang es una en la que nacieron el espacio, la materia y, de forma crucial, el tiempo. El espacio no apareci� de la "nada"; antes del momento de la creaci�n no hab�a "nada". El propio tiempo todav�a no hab�a empezado, y por ello ni siquiera tiene sentido hablar de un tiempo antes del Big Bang. Ni siquiera un Shakespeare o un Einstein podr�a explicar esto en lenguaje llano, �aunque una combinaci�n de los dos podr�a ser �til!

Se sigue tambi�n que cuando observamos hoy el Universo no tiene sentido preguntar "d�nde" sucedi� el Big Bang. El espacio s�lo naci� con el propio Big Bang. Por ello, en aquellas primeras pocas fracciones de segundo, el Universo entero que vemos hoy estaba en una min�scula regi�n, m�s peque�a que un n�cleo at�mico. El Big Bang sucedi� "en todas partes", y no hubo ning�n punto central.

Una bonita ilustraci�n de ello se da en un famoso grabado de Escher, conocido de forma no muy rom�ntica como Divisi�n Espacial C�bica. Imag�nese en uno cualquiera de los cubos que marcan las uniones en este ret�culo, mientras todas y cada una de las barras que unen los cubos se expanden. Desde su perspectiva parecer�a que todo se est� alejando de usted, y al principio parecer�a natural concluir que usted est� en una posici�n especial: el centro de expansi�n. Pero una reflexi�n le permite darse cuenta de que la expansi�n parecer�a igual en cualquier lugar del ret�culo en el que usted estuviera; no hay un centro. La situaci�n es muy similar en nuestro Universo; cada grupo de galaxias parece estar alej�ndose de nosotros, y pese a todo, los observadores que nos mirasen desde estas estrellas distantes ver�an la misma ilusi�n y presumiblemente concluir�an que est�n en el centro de la expansi�n.

Otro problema concierne a la pregunta frecuentemente planteada, y a primera vista razonable, "�qu� tama�o tiene el Universo?". Aqu� tenemos de nuevo un problema importante sobre el que parece haber dos respuestas posibles. O bien el Universo es de tama�o finito, o por el contrario no lo es. Si es finito, �qu� hay fuera de �l? La pregunta no tiene sentido; el propio espacio existe s�lo dentro del Universo, y por lo tanto no hay literalmente "fuera". Por otra parte, decir que el Universo es infinito es decir realmente que su tama�o no es definible. No podemos explicar el infinito en lenguaje cotidiano, y tampoco podr�a hacerlo Albert Einstein (nosotros lo sabemos, �porque Patrick se lo pregunt�!).

Recordemos tambi�n que tenemos que considerar el tiempo como una coordenada; en otras palabras, no podemos preguntar simplemente "�qu� tama�o tiene el Universo?", pues la respuesta cambiar� con el tiempo. Podr�amos preguntar "�qu� tama�o tiene el Universo ahora?" pero, como veremos m�s adelante, una consecuencia de la relatividad es que es imposible definir un �nico momento llamado "ahora" que tenga el mismo significado en todo el Universo.

Hablar de un Universo que tiene un tama�o concreto lleva inmediatamente a la idea de un l�mite. Si viaj�ramos suficientemente lejos, �topar�amos con una pared de ladrillo? La respuesta es no. El Universo es lo que los matem�ticos llaman finito pero ilimitado. Una analog�a �til es la de una hormiga arrastr�ndose por una bola. Viajando siempre en la misma direcci�n sobre esta superficie curva nunca llegar� a dar con una barrera, y puede recorrer una distancia infinita. Esto sucede a pesar del tama�o finito de la bola, de lo que la hormiga ser� completamente inconsciente. An�logamente, si estuvi�ramos en una potente nave espacial en lo que percibimos que es una l�nea recta, nunca llegar�amos al borde del Universo, pero esto no significa que el Universo sea infinito; veremos m�s adelante que tambi�n el espacio puede considerarse curvo.

Art�culo completo en El Cultural (Espa�a)